This post explores the Newton-Gregory interpolation method, an efficient algorithm for polynomial interpolation that’s particularly useful when dealing with equally-spaced data points. We’ll also see how it relates to Taylor polynomials.
Polynomial Interpolation Recap
As discussed in a previous post, we can find a polynomial that passes through a given set of points using various approaches. For a quadratic polynomial:
\[y = a_2 x^2 + a_1 x + a_0.\]Given 3 points \((x_0, y_0), (x_1, y_1), (x_2, y_2)\), we can solve for the coefficients using the system:
\[\begin{bmatrix} y_0\\ y_1\\ y_2\\ \end{bmatrix} = \begin{bmatrix} x_0^2 & x_0 & 1\\ x_1^2 & x_1 & 1\\ x_2^2 & x_2 & 1\\ \end{bmatrix} \begin{bmatrix} a_2\\ a_1\\ a_0\\ \end{bmatrix}\]The problem with this approach is that the Vandermonde matrix can be poorly conditioned. It also requires \(O(n^3)\) algorithmic complexity to solve which becomes relevant for higher order polynomials.
Alternatively, using the Lagrange basis functions:
\[\begin{align*} y &= a_0 {(x-x_1)(x-x_2) \over (x_0 - x_1)(x_0 - x_2)} + a_1 {(x-x_0)(x-x_2) \over (x_1 - x_0)(x_1 - x_2)} + a_2 {(x-x_0)(x-x_1) \over (x_2 - x_0)(x_2 - x_1)}\\ \quad\\ &= a_0 \ell_0(x) + a_1 \ell_1(x) + a_2 \ell_2(x)\\ \end{align*}\]By evaluating the polynomial at \(x_0, x_1,\) and \(x_2\), we get the trivial system of equations
\[\begin{bmatrix} y_0\\ y_1\\ y_2\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ a_2\\ \end{bmatrix}\]The strength of Lagrange interpolation is that finding the coefficients is trivial. You don’t need to implement complicated algorithms like Gaussian elimination or QR factorisation, just compute each coefficient directly.
A drawback of Lagrange interpolation however, is that we have no way of updating the coefficients. Say we were interpolating a regularly spaced time series and a new fourth point comes in. We’d then need a cubic polynomial, but with Lagrange, there’s no way to reuse the quadratic polynomial coefficients. We have no choice but to resolve for all of the coefficients.
Newton-Gregory Interpolation
Newton-Gregory is an alternative approach to polynomial interpolation that addresses some of the short comings of the previous two approaches.
Quadratic Case
The subject of this post is yet another parameterisation of the interpolating polynomial, this time given by
\[y = a_0 + a_1 (x-x_0) + a_2(x-x_0)(x-x_1)\]Enforcing that this polynomial pass through the points \((x_0, y_0), (x_1, y_1), (x_2, y_2)\) we get the system of equations
\[\begin{bmatrix} y_0\\ y_1\\ y_2\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 1 & x_1-x_0 & 0\\ 1 & x_2-x_0 & (x_2-x_0)(x_2 -x_1)\\ \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ a_2\\ \end{bmatrix}.\]If we make the further assumption that the points are evenly spaced with spacing \(h\) (as they might be when interpolating points from a lookup table), we get the following linear system
\[\begin{bmatrix} y_0\\ y_1\\ y_2\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 1 & h & 0\\ 1 & 2h & 2h^2\\ \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ a_2\\ \end{bmatrix}\]This triangular system makes forward substitution trivial, unlike the dense systems produced by the Vandermonde matrix
- From the first equation \(a_0 = y_0\)
- From the second equation \(y_1 = a_0 + ha_1 \implies a_1 = (y_1 - y_0) / h\)
- From the final equation, substituting in \(a_0\) and \(a_1\), \(y_2 = a_0 + 2 h a_1 + 2h^2 a_2 \implies a_2 = {y_2 - 2y_1 + y_0 \over 2h^2}\)
To make the pattern clearer, we can define backward difference operators. The first order backward difference operator is
\[\Delta y_i = y_i - y_{i-1}.\]We can also define a second difference operator as the backward difference operator applied to the backward difference
\[\Delta^2 y_i = \Delta (\Delta y_i) = \Delta (y_i - y_{i-1}) = y_i - 2y_{i-1} + y_{i-2}\]Using this notation we can rewrite our coefficients succinctly as
\[\begin{align*} a_0 &= y_0\\ a_1 &= {1 \over h}\Delta y_1\\ a_2 &= {1 \over 2h^2}\Delta^2 y_2\\ \end{align*}\]Substituting our coefficients back into the polynomial,
\[\begin{align*} y &= y_0 + {y_1 - y_0 \over h}(x-x_0) + {y_2 - 2y_1 + y_0 \over 2h^2}(x - x_0)(x - x_1)\\ &= y_0 + {\Delta y_1 \over h}(x-x_0) + {\Delta^2 y_2 \over 2h^2}(x - x_0)(x - x_0 - h)\\ &= y_0 +{x-x_0 \over h} \Delta y_1 + {x - x_0 \over h} {x - x_0 - h \over h}{\Delta^2 y_2 \over 2}\\ \end{align*}\]Defining the normalised distance from \(x_0\) as
\[u = {x-x_0 \over h},\]the polynomial simplifies to
\[y= y_0 + u \Delta y_1 + {u(u-1) \over 2} \Delta^2 y_2.\]General Case
The pattern for the system of equations might not be entirely obvious from the quadratic case, so let’s consider the case of a fourth degree polynomial
\[\begin{align*} y = &a_0 + a_1 (x-x_0) + a_2(x-x_0)(x-x_1) \\ &+ a_3(x-x_0)(x-x_1)(x-x_2) + a_4(x-x_0)(x-x_1)(x-x_2)(x-x_3) \end{align*}\]Plugging in evenly spaced points \(x_i = x_0 + i\cdot h\) and their corresponding \(y\)-values, \(y_i\), we get the following system of equations
\[\begin{bmatrix} y_0\\ y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 1 & h & 0 & 0 & 0\\ 1 & 2h & 2h^2 & 0 & 0\\ 1 & 3h & 3 \cdot 2h^2 & 3\cdot 2 \cdot 1 h^3 & 0\\ 1 & 4h & 4\cdot 3 h^2 & 4\cdot 3 \cdot 2 h^3 & 4 \cdot 3 \cdot 2 \cdot 1 h^4\\ \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ a_2\\ a_3\\ a_4 \end{bmatrix}.\]The entries of the matrix have the simple formula (assuming 1 based indexing)
\[a_{ij} = \begin{cases} 0 & i < j\\ {(i-1)! \over (i-j)!}h^{j-1} & i \ge j \end{cases}\]We can easily create this matrix with just a few lines of python
import math
import numpy as np
def create_matrix(n, h):
A = np.empty((n, n))
# zero based index rather 1 based in the previous formula
for i in range(n):
for j in range(i + 1):
A[i, j] = math.perm(i, j) * h**j
return AContinuing with forward substitution, we can easily find the coefficient of the cubic term is
\[\begin{align*} a_3 &= {y_3 - 3y_2 +3y_1 - y_0 \over 6h^3}\\ &= {1 \over 3!h^3}\Delta^3 y_3 \end{align*}\]The general form of the polynomial coefficients is
\[a_n = {1 \over n!h^n} \Delta^n y_n.\]Plugging back in, we get the Newton-Gregory interpolating polynomial
\[y = y_0 + u \Delta y_1 + {u(u-1) \over 2} \Delta^2 y_2 + {u(u-1)(u-2) \over 3!} \Delta^3 y_3 + \cdots\]where the general term is
\[{u(u-1)(u-2)\cdots(u-n+1) \over n!} \Delta^n y_n\]and the \(k\)-th order difference is \(\Delta^k y_n = \Delta^{k-1}y_n - \Delta^{k-1} y_{n-1}\). The following code shows an implementation of the Newton-Gregory method.
import math
import numpy as np
def bwd_diff(x, i: int, order: int = 1):
if i < 0:
raise ValueError(f"Index must be positive, got {i}")
if order < 0:
raise ValueError(f"Backward difference order expected to be >0, got {order}")
elif order == 0:
return x[i]
else:
return bwd_diff(x, i, order=order - 1) - bwd_diff(x, i - 1, order=order - 1)
def newton_gregory(x: np.ndarray, x_0: float, ys: np.ndarray, h: float) -> np.ndarray:
poly_order = len(ys) - 1
u = (x - x_0) / h
coeff = 1
result = np.zeros_like(x)
for k in range(poly_order + 1):
result += coeff * bwd_diff(ys, k, order=k)
coeff *= (u - k) / (k + 1)
return resultRelation to Taylor Polynomials
Recall the \(n\)-th degree Taylor expansion of a continuous function \(f\) about a point \(x_0\) is
\[\begin{align*} f(x) &= f(x_0) + f'(x_0)(x-x_0) + {f''(x_0)\over 2}(x-x_0)^2 + \cdots + {f^{(n)}(x_0)\over n!}(x-x_0)^n\\ &= \sum_{k=0}^n {f^{(k)}(x_0) \over k!}(x-x_0)^k . \end{align*}\]It turns out that Newton-Gregory interpolation is actually the discrete analog of Taylor polynomials!
Returning back to one of our expressions for the Newton-Gregory polynomial, we have
\[y = y_0 + {\Delta y_1 \over h}(x-x_0) + {\Delta^2 y_2 \over 2h^2}(x - x_0)(x - x_0 - h) + \cdots\]It is clear from the definition of the derivative that
\[\lim_{h\rightarrow 0} {\Delta y_1 \over h}(x-x_0) = f'(x_0)(x-x_0)\]Using the backward difference formulation of the derivative we have
\[f'(x_0) = \lim_{h\rightarrow 0} {f(x)- f(x-h) \over h}.\]Since the second derivative is simply the derivative of the first derivative
\[f''(x_0) = \lim_{h\rightarrow 0} {f'(x_0)- f'(x_0 - h) \over h}.\]By applying the backward difference approximation to the derivatives, we have
\[\begin{align*} f''(x_0) &= \lim_{h\rightarrow 0} {1 \over h}\left({f(x_0) - f(x_0-h) \over h} - {f(x_0-h) - f(x_0 - 2h) \over h}\right)\\ &= \lim_{h\rightarrow 0} {f(x_0) - 2f(x_0-h) + f(x_0-2h) \over h^2}. \end{align*}\]From this formulation of the second derivative, we can see that
\[\lim_{h\rightarrow 0} {\Delta^2 y_2 \over 2h^2}(x - x_0)(x - x_0 - h) = {1 \over 2}f''(x_0)(x - x_0)^2.\]Continuing with the higher order terms, we would see that in the limit as \(h\) approaches 0, the Newton-Gregory formula becomes exactly the Taylor polynomial.
Though Taylor polynomials use derivatives and Newton-Gregory uses finite differences, in the limit as the spacing tends to 0, differences become derivatives!
Figure 1 shows how the Newton-Gregory polynomial approaches the third order Taylor approximation of the logarithm as \(h\) decreases towards 0.
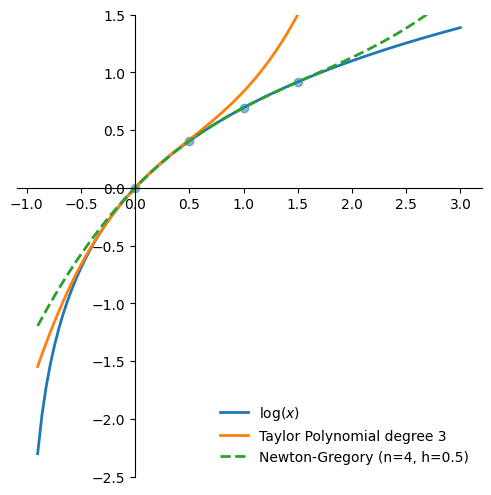
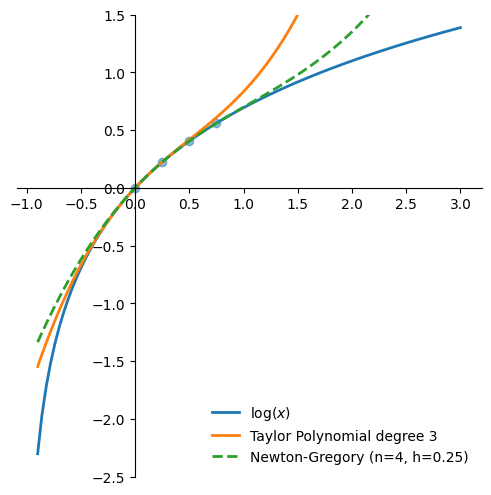
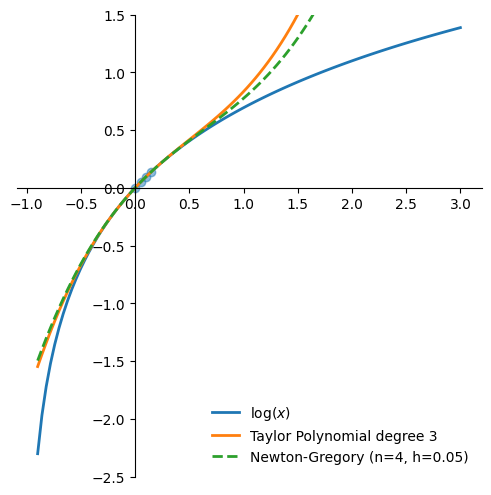
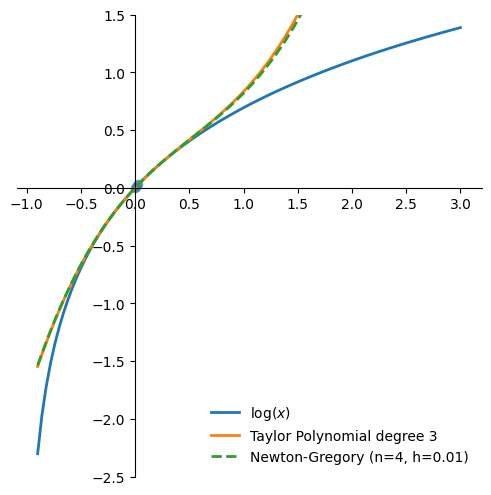
Conclusion
The Newton-Gregory method is useful when
- data is evenly spaced such as data from a numerical approximation table or time series sampled with a regular period
- new data points are arriving in an online fashion. Newton-Gregory allows you to solve for just one new coefficient without needing to resolve for the others.
- the Vandermonde matrix is ill-conditioned
In addition, Newton-Gregory interpolation provides a connection between discrete and continuous functions.
