Despite being one of the most familiar shapes, plotting ellipses is surprisingly difficult; being almost completely inaccessible to the uninitiated in linear algebra. The following post explores a few different representations of ellipses and how to plot them.

Ellipses

Conic Form

The most common definition of the ellipse is usually encountered when studying conic sections somewhere around 10th grade. The conic form of the ellipse is given by

\[\begin{align*} Ax^2 + Bxy + Cy^2 + Dx + Ey + F &= 0\\ B^2 - 4AC &< 0 \end{align*}\]

where the quantity \(B^2 - 4AC\) is called the discriminant of the conic section. Evidently, this form is not particularly amenable to plotting software such as matplotlib since \(y\) is defined implicitly for each value of \(x\) rather than being an explicit function of \(x\).

Quadratic Form

It is a simple exercise in matrix multiplication to verify the conic representation presented above is equivalent to the following equation

\[\begin{align*} z^TQz + b^Tz + F = 0\\ Q\in \mathbf{S}^2_{++} \end{align*}\]

where

\[\begin{align*} Q = \begin{bmatrix} A & B/2\\ B/2 & C \end{bmatrix}, \, b = \begin{bmatrix} D \\ E \end{bmatrix}, \, z = \begin{bmatrix} x \\ y \end{bmatrix} \end{align*}\]

The constraint \(Q\in \mathbf{S}^2_{++}\) is a more compact way of saying that \(Q\in \mathbf{R}^{2\times 2}\), \(Q=Q^T\), \(\mathbf{det}\, Q > 0\), and \(\mathbf{trace}\, Q\).¹

Recall that completing the square for a single variable quadratic \(ax^2+bx+c=0\) requires adding and subtracting \(\frac{b^2}{4a}\) in order to eliminate the linear term

\[a(x - b/2a)^2 + c - b^2/4a = 0,\]

Analogously, this can be accomplished in the multidimensional case by adding and subtracting \(\frac{1}{4}b^TQ^{-1}b\), yielding

\[\left(z - \frac{1}{2}Q^{-1}b\right)^TQ\left(z-\frac{1}{2}Q^{-1}b\right) + F - \frac{1}{4}b^TQ^{-1}b = 0\]

Provided we do not have a degenerate case in which \(F - \frac{1}{4}b^TQ^{-1}b = 0\), this can be rewritten in an even more compact form²

\[(z - c)^TP(z-c) = 1\]

This is an ellipse expressed as a quadratic form.³ Note that if \(P=r^{-2}I\), this reduces to a circle with radius \(r\). When \(P=\mathbf{diag}(1/a^2, 1/b^2)\), we have the familiar equation of an axis aligned ellipse

\[\frac{(x-x_c)^2}{a^2} + \frac{(y-y_c)^2}{b^2} = 1\]

Though mathematically simple, this equation is still not amenable to plotting as there is no simple way to get all the valid \(x,y\) pairs satisfying it.

Parametric Form

Since \(P\) is symmetric, the spectral theorem guarantees the matrix can be diagonalised as \(P=V\mathbf{diag}(\lambda_1, \lambda_2)V^T\) where \(V^T=V^{-1}\). Since an ellipse is the set of points

\[\{z : (z-c)^TP(z-c)=1\}\]

we can substitute the factorised form for \(P\) to arrive at an alternative representation

\[\{z: (z-c)^TV\mathbf{diag}(\lambda_1, \lambda_2)V^T(z-c) = 1\}\]

Since the eigenvalues are positive (by the assumption that we have an ellipse), this is seen to be equivalent to the following set

\[\left\{z: \lVert\mathbf{diag}\left(\lambda_1^{1/2},\lambda_2^{1/2}\right)V^T(z-c)\rVert^2 = 1\right\}\\\]

Setting \(u = D^{1/2}V^T(z-c)\)

\[\left\{z: z = V\mathbf{diag}\left(\lambda_1^{-1/2}, \lambda_2^{-1/2}\right)u + c,\, ||u||^2 = 1\right\}\\\]

This description, though less elegant than the quadratic form, contains the exact instructions of how to plot an ellipse.

The so-called parametric form of the ellipse gives the following algorithm for creating an ellipse

Create a unit circle \(\{u: \lVert u\rVert^2=1\}\).
Stretch the unit circle by \(\lambda_1^{-1/2}\) in the \(x\) direction and \(\lambda_2^{-1/2}\) in the \(y\) direction. Equivalently, apply the linear transformation \(D^{-1/2}=\mathbf{diag}\left(\lambda_1^{-1/2}, \lambda_2^{-1/2}\right)\).
Rotate this axis aligned ellipse by pre-multiplying with the matrix \(V\). Recall that \(V^{-1}=V^T\) so \(V\) represents a rotation and/or reflection.
Translate the ellipse away from the origin by adding the vector \(c\).

The steps in the transformation are illustrated in the animation below

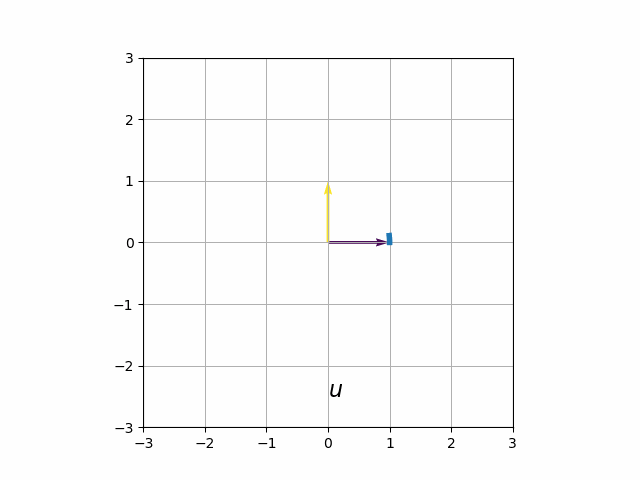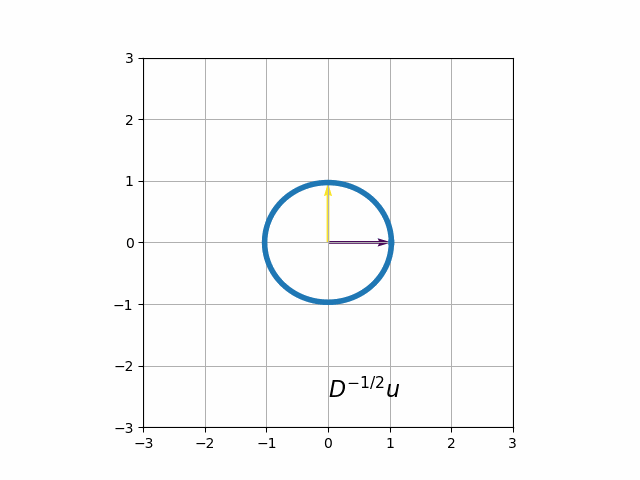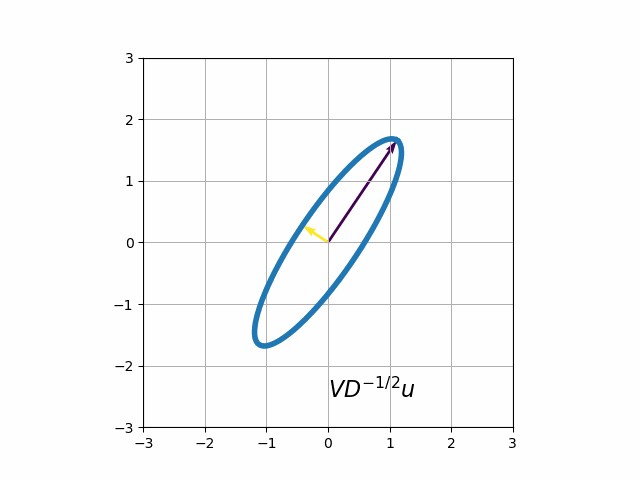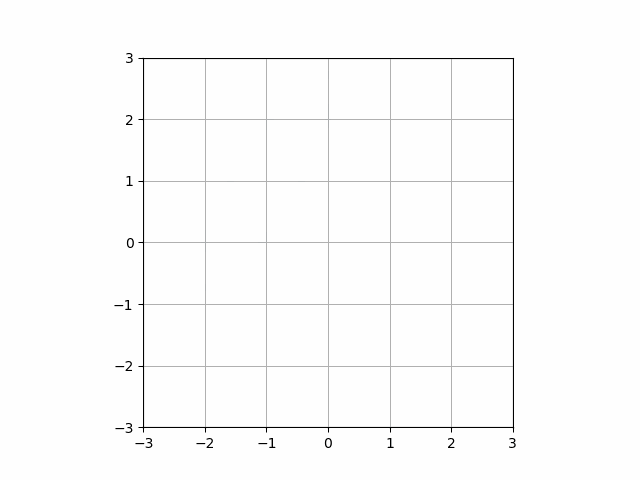
Ellipse Plotting

`plt.contour`

By far the easiest way to plot an ellipse is to use the contour function provided in matplotlib. First, create an \(x,y\) meshgrid as with any contour plot. Then call the contour function and ensure the level parameter is set to 1 (if in conic form then it should be set to 0)

import numpy as np
import matplotlib.pyplot as plt

def plot_ellipse_contour(
  P: np.ndarray,
  c: np.ndarray,
  n_points: int = 50,
):
    x = np.linspace(-2, 3, n_points)
    y = np.linspace(-3, 1, n_points)

    X_mesh, Y_mesh = np.meshgrid(x, y)

    # 2 x n_points^2
    xy_points = np.row_stack([X_mesh.ravel(), Y_mesh.ravel()]) 
    xy_centered = xy_points - c

    z = (xy_centered * (P @ xy_centered)).sum(axis=0)
    Z_mesh = z.reshape(X_mesh.shape)
    plt.figure()
    plt.contour(X_mesh, Y_mesh, Z_mesh, levels=[1])

There are a couple reasons this method is of limited use in practice. First, given an arbitrary quadratic or conic form ellipse, it is impossible to know boundaries in which the ellipse lies. This leads to a lot of guess and check when creating the meshgrid. The second issue is that the sampling efficiency is extremely poor. When drawing samples on a grid, most of the points created in the meshgrid are unnecessary. That is to say, very few of the \((x,y)\) pairs created in the sampling grid lie anywhere near the ellipse itself.

`matplotlib.patches`

To be sure, matplotlib does provide a helper utility for plotting ellipses under matplotlib.patches. However, it requires a center, height, width, and angle parameter. An ellipse is almost never given in this form. In fact, if you are willing to go so far as to derive these quantities, you are better served plotting it yourself.

Parametric Plotting

In the preceding section, it was found that an ellipse can be generated as long as we have the ability to plot a unit circle and compute the eigen decomposition. The algorithm for plotting an ellipse in this way is summarised as follows

Compute the eigenvalue decomposition \(VDV^T\) of \(P\).
Form a vector \(\theta \in \mathbf{R}^N\) with values \(0 \le \theta_i < 2\pi\).
Create vectors \(x\in\mathbf{R}^N\) and \(y\in\mathbf{R}^N\) where \(x_i = \cos \theta_i\) and \(y_i = \sin \theta_i\). These points lie on the unit circle.
For each point on the unit circle, \([x_i, y_i]^T\) multiply on the left by \(VD^{-1/2}\)⁴ and add \(c\).

This routine is expressed using numpy in the code below

import numpy as np
import matplotlib.pyplot as plt

def plot_ellipse_parametric(
  P: np.ndarray,
  c: np.ndarray,
  n_points: int = 100,
):
  eig_vals, V = np.linalg.eigh(P)
  D_inv = np.diag(np.reciprocal(eig_vals))

  theta_points = np.linspace(0, 2 * np.pi, n_points)
  xy_unit_circ = np.row_stack([np.cos(theta_points), np.sin(theta_points)])
  xy_points = (V @ np.sqrt(D_inv) @ xy_unit_circ) + c
  x_points = xy_points[0, :]
  y_points = xy_points[1, :]

  plt.figure()
  plt.plot(x_points, y_points)

Applications

Below are some examples of cases in which ellipses arise in applications.

Confidence Ellipses

A Gaussian random vector with mean \(\mu\in \mathbf{R}^n\) and covariance \(\Sigma\in \mathbf{R}^{n\times n}\) has density

\[f_X(x) = (2\pi)^{-n/2}|\Sigma|^{-1/2} \exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)\]

For hypothesis testing, it is of interest to just look at the random variable in the exponent

\[z = (x-\mu)^T\Sigma^{-1}(x-\mu) .\]

This variable has chi-square distribution with \(n\) degrees of freedom. Since covariance matrices have nonnegative eigenvalues, the level sets clearly define ellipses as quadratic forms. They are aptly named confidence ellipses. Given a particular level set, the interior defines a space in which a random draw from \(f_X(x)\) has a specific probability of landing. The probability of a gaussian random vector lying in this ellipse is in fact dictated by the chi-square distribution.⁵

Least Squares

An ordinary least squares (OLS) problem is defined by

\[\begin{equation} \underset{x}{\text{minimize}} \quad ||Ax - y||^2 \end{equation}\]

with \(A\in \mathbf{R}^{m\times n}\), \(y\in\mathbf{R}^m\). Expanding out the objective we have

\[f_0(x) = x^TA^TAx + 2y^TAx + y^Ty.\]

Since it can be shown that \(A^TA\) will always have non-negative eigenvalues, the level sets of the objective \(f_0\) define ellipses (when \(n=2\)).

Conclusion

Ellipses appear in a number of places, both pure and applied. The code provided should make it a simple exercise to move between ellipse representations as well as provide some simple code for plotting an arbitrary ellipse.

Footnotes

1: More generally, \(Q\in \mathbf{S}^n_{++}\), means that \(Q\) is a positive semidefinite matrix. When \(n=2\), a positive determinant is sufficient to ensure this. In fact, it is identical to the discriminant condition.

2: Here, \(c=Q^{-1}b\) is the center of the ellipse and \(P = Q/(\frac{1}{4}b^TQ^{-1}b - F)\).

3: Some author’s use the convention \((z-c)^T P^{-1} (z-c)\) instead.

4: This is called the coloring matrix. Additionally it is \(P^{-1/2}\), the inverse of the matrix square root of \(P\)

5: If the ellipse is defined by \(\left\{x| (x-\mu)^T\Sigma^{-1}(x-\mu) \le \alpha\right\},\) then a random draw of \(x\) will have probability \(F^{-1}_{\chi_n^2}(\alpha)\) of being inside the region.\(\, F^{-1}_{\chi_n^2}\) is the inverse CDF of a chi-square distribution with \(n\) degrees of freedom.

Twitter Facebook LinkedIn

Plotting Ellipses

Casey Haaland